
THE DESIGN OF THE HUMAN BEING
Keywords
discrete, equation, evolution, fractal, human, mind's eye, paleoanthropology, sentence, symmetry, technology, Wigner
Abstract
Internal structures and processes in the design of a human being are hidden. We are thus presented with two mysteries. The first concerns the structures and processes themselves. The second concerns the mechanism that hides them, and the reason for hiding them. I propose here a complete, coherent theory of the human being under a fractal-cascade system. The fundamental mechanism of the human being consists of discrete symbols attached to the branches of a repeatedly bifurcating fractal tree. This mechanism alone is enough to generate the equation, and, when modified into an asymmetrical condition, the common sentence. Much of our subjective experience is a matter of internally generated categories acting as perceptual substitutes for physical events, as when sensations of color replace wavelengths of light in experience. Thus power-of-assertion is a perceptual replacement for the symmetry of the fundamental fractal, while sense-of-truth-and-falsity is a perceptual replacement for the symmetrical or asymmetrical relationship between the symbols attached to its two sides. Technology is a re-enactment, in physical terms, of the sentence — transforming one image into another. The use of the mind's eye in technology is a mobilization of the physics and geometry represented by the equation. The human being emerged when the sentence invaded voluntary animal actions, transforming them into proxy sentences. Sense-of-purpose is a perceptual replacement for power-of-assertion in deliberate action; and sense-of-right-and-wrong is a replacement for sense-of-true-and-false. Through cascades of perceptual replacement, then, meaningful experience is generated, starting from the remote and abstract, but basic properties of symmetry and discreteness.
INTRODUCTION
By reinterpreting old observations and introducing new ones under a single system, a complete, coherent theory of the human being becomes possible. The human being can be understood as a kind of engine that makes remarkably sophisticated use of remarkably simple means, i.e., it generates meaningful experience out of the interaction between two core faculties, one static, the other dynamic.
The dynamic system consists of a repeatedly bifurcating, symmetrical fractal tree (Abler 2013, Figures 4,5,6), with the same dynamic geometry as a lightning bolt or nuclear chain reaction. This dynamic fractal is the fundamental mechanism of the human brain. It generates the structure upon which language, mind, technology and deliberate action are built, but it is a fleeting process, like a lightning bolt, not a stable object, and is not noticed.
The static system (Abler 1989) consists of discrete or particulate symbols that are attached to the branches of the developing fractal tree. The discrete nature of these symbols gives them permanence, allowing them to be noticed and remembered, and creating the illusion that the entire structure is resident in the symbols. See Figure 1.
We can manipulate only those structures of which we are aware. But through a process of sensory substitution, our perceptual system enables us to generate meaningful experience from geometric properties that are abstract and remote, and not obviously related to our strongly held concepts of power-of-assertion, true-and-false (Abler 2010), good-and-bad, beautiful-and-ugly, and sense-of-purpose.
The critical difference between human beings and other animals is that human beings possess language, in other words they possess sentences. Thus any concept of the human being begins from the mechanism that generates the sentence; and any other beginning assumes the proof and begs the question. A brief review of the sentence follows.
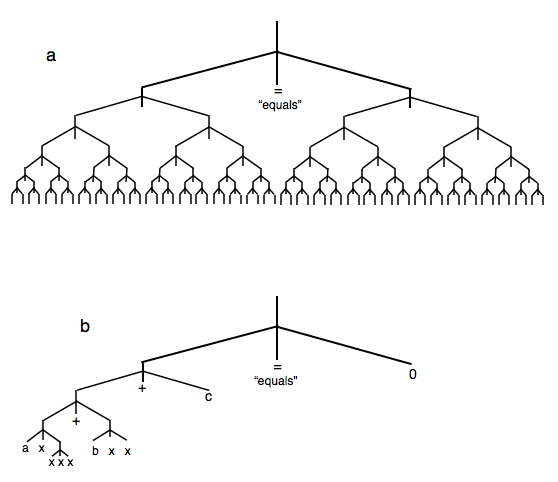
Figure 1. The fundamental mechanism of the human brain has the same inorganic geometry as a river system or lightning bolt or nuclear chain reaction, as shown in idealized form at a. By itself, this repeatedly bifurcating, symmetrical fractal is enough to generate the equation. The axis of symmetry is represented by the "equals". b: Arithmetical operators +, -, are defined by the axes of subordinate fractals. Numbers and variables are attached to the fractal branches. The fractal stops growing where the symbols are attached. Shown here is the development of the equation "ax2 + bx + c = 0". By covering the Figure with a sheet of paper, and sliding the paper slowly downward, the fractal tree is gradually revealed, thus simulating its dynamic development in the brain. Like the branches of a lightning bolt, the fractal tree fades as soon as it forms, leaving only the discrete symbols in their linear order. Figure re-conceived after Abler 2013, Figure 6.
THE SENTENCE
A sentence is transmitted in the form of a linear string of discrete items, the phonemes. Under the "particulate principle of self-diversifying systems" (Abler 1989), or law of discrete emergence, discreteness is a necessity because blending constituents would combine into an undifferentiated signal. Each such signal could be unique as-a-whole, but would not have differentiated components: It would have to be memorized as-a-whole in advance, i.e., discreteness is a necessity both for the creation of sentences in large numbers, and for their spontaneous use. Equations are sentences.
A sentence is not a given object to be described, but a system whose derivation is to be understood. A sentence is generated and defined by attaching discrete words to the branches of a dynamically developing fractal tree (see Figure 2, and Abler 2013, Figure 6) that has the same bifurcating geometry as a river system, or lightning bolt, or nuclear chain reaction. The fractal tree — not the equation or the common sentence — is thus spontaneously occurring, self-organized, pre-biological and inorganic, and can be taken as given. The fractal branches are dynamically symmetrical, and their symmetry defines the equation.
ASYMMETRY OF THE INFRASTRUCTURE
The fractal tree is the shared infrastructure of the equation and the everyday sentence. But the introduction of asymmetry to the infrastructure introduces two properties, syntax and access to universal vocabulary, that create the common sentence and, ultimately, language and the human being. First, the equation is formed and defined by the property of symmetry and repeated symmetry, and is limited to assertions in mathematics, because only numbers intrinsically express symmetry. For example, "√4=2" is symmetrical and meaningful within arithmetic, and is the same as "2=√4". But with no assertion of symmetry, the common sentence is free to accept non-numerical concepts. Second, the introduction of asymmetry to the infrastructure introduces meaning to word order, thus introducing syntax. For example "John ate the alligator" and "The alligator ate John" are not the same. (Abler 2005, p. 83; 2010, p. 413; 2013, p. 54). The symmetrical fractal tree is spontaneously-occurring, and its potential use in mathematics was exploited only after the common sentence was already old in human history.
PERCEPTUAL SUBSTITUTION
Many human sensations, such as sensations of color or of tone, are a matter of substituting an internally-generated category such as green or A-440, for some process in physics, such as disturbances of air pressure or of electrodynamic frequency, of which we are never aware. The idea of sensory substitution incorporates, into a general theory, what Liberman et al. (1967, p. 441) called the "speech mode" of auditory perception: the substitution of internally generated categories, the phonemes, for incoming acoustic events. Phonemes are numbers (Abler 2013, Figure 9), but a process of replacement causes them to be perceived as the sounds of speech, with their own intrinsic logic and esthetics.
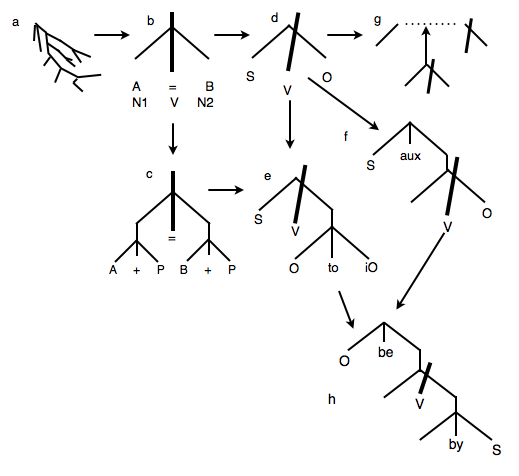
Figure 2. Equations and common sentences generated by modification of a simple inorganic fractal. a: A bifurcating fractal generated by sending an electric spark into a block of lucite. The branchings are energetically symmetrical. ("Captured Lightning" made by B. Hickman.) b: A single fractal unit re-drawn in geometrically symmetrical form. This fractal generates the rudimentary equation "A=B". c: A second fractal tier generates the arithmetical operators, and the equation "A+P=B+P". d: The common Subject-Verb-Object sentence, generated by tilting the axis of symmetry off-center (Abler 2010). e: A second fractal tier generates the Indirect-Object sentence. f: Embedding one fractal subunit below another generates the auxiliary "will", "might", "could", and other constructions. g: Syntactic embedding is a matter of inserting one fractal unit into another. (After Abler 2013, Figure 8). h: Passive voice is generated by combining e and f. Once established in a language, such patterns as the above may become standard "hardware", not generated new each time they are used.
The human power of assertion is expressed only in declarative sentences, i.e., in equations and common sentences. The process of generating an equation "a=b" from the property of symmetry simultaneously generates the concept of making a statement, or assertion, i.e., the primitive assertion (Abler 2010, p. 412) is, "a and b are equal to one another", in other words, "I am symmetrical". Thus the concept of assertion is a perceptual substitution for the symmetry that generates the rudimentary sentence. The truth-or-falsity of statements in arithmetic depends on the symmetrical or asymmetrical relationship between the symbols attached to the two sides of the symmetrical infrastructure, because such symbols either do or don't stand in a symmetrical relationship to one another. If the sense of truth-and-falsity had evolved by natural selection, a cause-and-effect relationship would hold between objective truth and perceived truth. Superstitions, prejudices, myths, red-herrings, and "armchair" tests such as the "true believer" or "consider the source" would be inconceivable, yet we are surrounded by them (after Abler 2010, p. 420). The concept of truth-or-falsity is a perceptual substitution for the geometry of the symbols attached to the equation fractal. Power-of-assertion and sense-of-truth-or-falsity are retained in the common sentence. As the first and universal products of the equation's inorganic geometry, assertion and truth-and-falsity are the original capabilities of the human mind, and are aspects of the same thing.
SENTENCE PROXIES
We possess a small but constantly used inventory of proxy sentences in the form of gestures which are standard usage in certain commonly-recurring situations: Holding out a thumb to hitch a ride, tapping a foot to show impatience, winking an eye to show mutual understanding. Despite the small number of such gestures (about 30 that would be recognized in America. See Table 1), the diversity in their meanings and use of anatomy, and the ease with which they are learned and understood, shows that the mechanism for their creation and use is close to the surface, and can be mobilized whenever a commonly-recurring situation is noticed. Such ready and universal access is possible only because the mechanism for their creation consists of an already-existing system under which all human acts, including and especially those that are performed silently, are proxy sentences. Gesture-sentences are produced on the model of these. This is not a matter of sign language, whose gestures are mostly words, or of the gestural theory of the origin of language, or the observation that people are constantly talking about what they are doing while they are doing it, but the concept that all human acts are proxies for the basic sentence with its unique power of assertion and property of truth-or-falsity.
29
- Thumb out: "I want a ride."
- Tapping a foot: "I am impatient."
- Winking an eye: "We understand each other."
- Hands up: "Don't shoot."
- Roman thumbs up: "Let him live."
- Roman thumbs down: "Let him die."
- Modern thumbs up: "This is OK."
- Modern thumbs down: "This is not OK."
- Thumb and index finger form a circle: "This is perfect."
- Twirling finger beside head: "He is crazy."
- Thumb and little finger beside head: "You have a telephone call."
- Fingers crossed: "It is OK to tell a lie."
- Arm up: "I will make a right turn."
- Arm out: "I will make a left turn."
- Arm down: "I will stop."
- Nod: "Yes, I agree."
- Shake head: "No, I disagree."
- Waving a hand at a driver or pedestrian: "I will wait for you to cross."
- Rubbing thumb against 1st and 2nd fingertips: "You owe me money."
- Index finger to lips: "Be quiet."
- Curling index finger: "Come here."
- Hands clasped: "I hope and pray."
- Index finger raised: "Wait a minute."
- Index finger drawn across throat: "You might be killed."
- Repeated tapping on a person: "Stop!" (in wrestling)
- Pointing at an item: "How much is that?" (at a flea market)
- Hand oscillating: "I am not sure."
- One eyebrow raised: "I disapprove."
- Holding one's nose: "This stinks."
- Rolling eyes: "This is ridiculous."
- Slapping forehead.: "I made a mistake"
- Zipping lips: "Keep quiet."
Table 1. Sentence proxies. The Table shows discrete, unitary gestures that are understood as complete sentences, and whose function is to substitute for such sentences in real-life situations.
WHAT PEOPLE DO
The human sense, then, of purpose or intent is our perceptual substitution for the power of assertion that the sentence lends to all human acts. The human sense that one act is good while another is bad, is our perceived substitution for the property of truth-or-falsity that the sentence lends to all human acts. Thus we find a cascade of substitutions: symmetrical /asymmetrical — true/false — good/bad. The good/bad opposition generates its own cascade of oppositions: right/wrong; moral/immoral, and others.
HUMAN TECHNOLOGY
Humans are arguably dependent on technology for their existence. Like other human actions, human technology is a proxy for sentences, in other words, technology requires the use of deliberate acts for the manipulation of material. But at a second, more basic level, human technology starts from a system of mental images that are of no immediate biological interest. Lost-wax casting, for example, not to mention the direct construction of negative molds (Abler 1973, p. 73ff), or the ability to handle objects under a microscope, require people to summon images that have their source in geometry, not in biology. There would have been no call for such images during the formative period, yet plenty of modern people can use them. Thus where animals have evolved to see external objects as manifestations in biology, people see such objects as manifestations in geometry and physics. A dog might see the wheel of a moving bicycle as a running animal, for example, and chase it and bite it; or a gorilla might see a rope as a snake, but people see such things on their own terms. How, then, did geometric-physical images find their way into the human mind?
LEMMA ON WIGNER’S (1960) “UNREASONABLE EFFECTIVENESS”
Ever since Pythagoras, sixth century B.C., it has been noticed that the properties of mathematics, whose founding and central structure is the equation, are a mirror of the properties of physics; and from this we might take for granted that the geometry in the mind's eye is a perceptual substitution for the geometry corresponding to the equation. But to be sure that the relationship of the equation to geometry and physics is a matter of principle, and not of luck, or simple hard work, a theory is needed. Any theory of mathematics, then, begins by showing the mechanism that generates its most elementary structures, the equations, "a=b", and "1+1=2" (Abler 2010, p. 413ff; and Figure 2); and any other beginning assumes the proof and begs the question.
Mathematics is a mirror of physics because equations and physics events intersect in the properties of symmetry and isolation. Thus symmetry determines that each side of the equation responds to changes in the other side only, not to changes in the surroundings (Abler 2010, p. 413). That is what is meant by "doing the same thing to both sides". Thus "2+2=4" at the Equator or at the North Pole, day or night, whether solved by man or woman, rain or shine. A step in a mathematical derivation is "correct" when symmetry is maintained from one expression to the next. The isolation resulting from symmetry causes the equation to be self-regulated and self-determined, and found — not made. Equations are thus intrinsically true or false, while common sentences retain the property of assertion, but their truth-and-falsity is not intrinsic. Compare the assertion "Two and two is four" to the assertion "Oatmeal is delicious", or "Marlowe wrote Shakespeare".
Under Newton's Third Law, "For every action there is an equal and opposite reaction", events in physics are intrinsically symmetrical. To take an example from Newton's day, the firing of a cannon should send the cannonball and the cannon itself in opposite directions with equal momentum. And the more nearly isolated the physics event, or experiment, is from its surroundings — from friction with the air, from gravity, from friction in the bearings, rolling resistance, leakage between the cannonball and the bore, or through the touch-hole — the more nearly the experiment approaches to Newton's symmetrical ideal, until we arrive at the thought-experiment. An example from our own day might be the energetically symmetrical paths of particles in a bubble chamber. Equations, then, are isolated because they are symmetrical, while physics events are symmetrical when they are isolated.
THE MIND’S EYE
The mental images used in technology function identically to those used in sentences (Abler 2005, p. 93; 2010, p. 408). Using the mind's eye (Abler 1973, p. 109), the craftsman begins with an image of the starting material, and an image of the finished product, and formulates from these a linear plan, incorporating an image of a tool, that transforms the first image into the second. The speaker likewise starts from a mental image of what the listener knows, and of what the speaker wants the listener to know — and formulates from these a sentence, or tool, that leads the listener from the first image to the second. The equation comes first because its structure is generated directly by attaching symbols to a spontaneously occurring, inorganic structure, its underlying fractal geometry. The mind's eye is a sensory substitution for the geometry and physics that correspond to equations. The imagery of technology is a sensory substitution for equations, while imagination is a sensory substitution for common sentences. Technology itself is a reenactment, in physical terms, of the sentence.
CONSCIOUSNESS
Consciousness, as human beings experience it, is the internally generated sensation that our perceptual system substitutes for power-of-assertion and sense-of-truth-or-falsity in combination, because such a system forces us to see that we are responsible for what we do. In other words it forces us to view our acts as autonomous entities that are produced by us, yet are whole and apart from ourselves.
HUMAN EMERGENCE
Humanization, the process by which our animal ancestors were transformed into human beings, then, is a matter of the sentence infrastructure invading, occupying, colonizing and inhabiting animal actions, transforming them from voluntary movements into deliberate human acts. As a result of the sentence invasion, all human acts are proxy sentences. This is why human beings are responsible for what they do in a way that other animals are not: Lacking sentences and the internally-generated substitutions for them, machines and non-human animals lack consciousness, deliberate action, sense of purpose, concept of assertion, concept of true-or-false, sense of right-and-wrong, and responsibility for what they do. Nonhuman animals lack mental images corresponding to devices in technology, and interpret mechanical motion as a living thing. But the first question of humanization is this: What caused the symmetrical fractal to become asymmetrical, thus opening the way to the common sentence and the human being?
DISCUSSION
There is no grand synthesis. Human complexity is not original, but represents proliferations of simple structures generated by the static-dynamic mechanism, which is original, as shown in Figure 2. The concept of psychology as it applies to the human being will have to be re-thought in light of the sentence and its substitutions and proliferations. Thus the iconic human face, which serves as a kind of passport, and the human form with its ideal of beauty, has the character of assertions expressed through the action of sexual selection on the basis of preferred mental images. The sense of beauty itself is an nth-degree perceptual substitution for the symmetry with which it is still sometimes confused. The human being will not be understood by working haphazard or piecemeal, i.e., "one more piece of evidence" misses the point. The bones and stones and works-of-art of paleoanthropology, and the relationship of phenotype to genotype, as well as the organization of the human brain, will be understood in light of a consistent theory; and a consistent theory will inform productive experiments — not the other way around, because every fact and every experiment is judged on the basis of theory, whether expressed or implied.
Language is a sister of algebra. The phonemes of language share a common source in nature with the digits. The words of language share a common source with the numbers. The "equals" or axis of symmetry shares a common source with the main verb. The arithmetical operators +, −, ×, ÷ share a common source with the prepositions. And the sentences of language share a common source with the equation. These are the only original components of mathematics and language, identified by method. Sensory replacement prevents us from seeing these relationships intuitively. And the sentence, pervading and permeating every human action, defines the human being with its intrinsic power of assertion and sense of truth-and-falsity, which represent the first properties of mind, also identified by method. The bright spark that illuminates human life beyond that of any other animal becomes possible by attaching discrete concepts to the equation-sentence fractal, thus placing them into meaningful relationships with one another. If there is continuity with other animals, it lies here.
The above findings suggest three further questions. The first is to find the chain-reaction that generates the equation fractal in the brain. Such a fractal is not necessarily generated by transmission of a signal from one nerve cell to the next through axons, but may be propagated from one synapse to the next extracellularly and inorganically before being "captured" by nerve cells. Further, the fractal may have undergone transformations that make it difficult to identify. The demonstration of such a fractal in any brain, even that of a flatworm, would show that the raw material for the production of equations is primitive, and that the human brain merely found a way to exploit it in the production of equations and common sentences.
The next question concerns the phonemes of language and the digits of arithmetic. While there is, in principle, no upper limit to the number of phonemes in any given language, in practice their number is limited by the acoustic geometry of the speech signal, or the "phonetic space" that can be maintained between the speech articulations (Peterson & Barney 1955; Liberman et al. 1967; Abler 2005, p. 64ff). The speech articulations are thus not phonemes, but only the addresses of phonemes. Constrained by the limits imposed by physics, the articulations and their acoustic consequences arrange themselves in serial order according to a periodic law (Abler 1989, Figure 3; 2013, Figure 9). But the phonemes themselves are not obviously arranged in any order, and are not obviously physical manifestations at all. The phonemes, then, and, by extension, the numbers, are thus unexpectedly abstract and mysterious. The non-physical symmetry of the equation is likewise a profound mystery.
The last question concerns the geometry of the dynamic equation-sentence fractal and the static symbols that are attached to it. Theoretical advances are sometimes made by resolving apparent paradoxes in our observations. If we assume that the discrete, or static components and the fractal, or dynamic components of the equation are manifestations of the same thing, the resolution of the static/dynamic paradox may lead to a deeper understanding of mathematics and matter. In somewhat the way that the atom generates a rich and varied world out of empty space and almost no material, the human perceptual engine generates a rich and varied experience out of the remote and abstract, and, in themselves, almost meaningless properties of discreteness and symmetry.
ACKNOWLEDGMENTS
I thank J. Wine, C. Freeman, P. Tobias, and C. Knox for comments; and M. Schwan, L. Schmidt and C. Lee for assistance.
REFERENCES
Abler B (1973) The Sensuous Gadgeteer (later Shop Tactics). Running Press, Philadelphia
Abler WL (1989) On the particulate principle of self-diversifying systems. J Soc Biol Struct 12:1-13
Abler WL (2005) Structure of Matter, Structure of Mind. Pensoft, Sofia; BainBridgeBooks, Philadelphia
Abler WL (2010) The human mind: origin in geometry. Sci Prog 93:403-427
Abler WL (2013) On isolating, identifying and defining the uniquely human component of mind. Cog Crit UMN 7:49-69.
Liberman AM Cooper FS Shankweiler DP Studdert-Kennedy M (1967) Perception of the speech code. Psych Review 74:431-461
Peterson GE Barney HL (1952) Control methods used in the study of vowels. J Acoust Soc Amer 24:175-184
Wigner EP (1960) The unreasonable effectiveness of mathematics in the natural sciences. Comm Pure Appl Math 13:1-14