Structure and Organizational Principles of Agile Behavior: Challenges and Opportunities in Cognitive Engineering
Bernie Mettler
College of Science & Engineering
University of Minnesota
Minneapolis, Minnesota
Email: mettler@umn.edu
Accepted 25 January 2011
Keywords
spatial behavior, trajectory, agility, navigation, cognition, planning, dynamics
Abstract
The elaborate agile spatial control skills of humans and many animals are not fully accounted for in the cognitive sciences. At the same time, engineering faces challenges in developing methodologies beyond traditional tracking and regulations functions that would lead toward improved adaptation and flexibility. The role of cognitive functions in spatial behavior has traditionally been focused on planning and memorization required for simple forms of navigation. However, observation of humans and animals performing spatial control tasks under competitive conditions requiring agile and adaptive behavior suggest more elaborate cognitive dimensions. These dimensions support the fine-tuned maneuvering and guidance behavior based on a broader understanding of the task and environment. This understanding must encompass more than the topology of geographical space but also take into account the dynamics of movement and a dynamic fit between behavior, environment and task. Here I highlight this gap and bring attention to these additional cognitive dimensions. In particular I suggest that agile behavior must be based on, and operate within, some structure that is inherent to the dynamic interaction between the agent and its environment. I argue that these structures are central to cognition. They provide a physically consistent link between the high-dimensional, nonlinear physical nature of movement and the discrete, lower-dimensional space typically associated with tactical reasoning. These structures can be understood as a semantic basis for abstraction. Finally their internal, organizational principles would also provide a functional basis for mechanisms needed for learning and adaptation. I conclude with avenues to understand the structure and organizational principles of agile behavior based on principles of dynamics and optimal control.
Agility in Humans and Machines
Skilled helicopter pilots can negotiate complex spatial environments while exploiting the full capabilities of their vehicle; they can adapt their behavior to adverse flight conditions, while simultaneously incorporating prior knowledge of the environment or task. Proficient pilots do not follow a set of scripted instructions but continuously adapt their plan based on the immediate environment, the available information about the larger environment and the flight conditions. Under favorable conditions, they can exploit a vehicle's full physical capabilities. In the presence of uncertainties about the environment or disturbances, they conservatively adapt performance to mitigate risks. This adaptation is not only limited to the level of performance but also encompasses the broader knowledge of the environment and task. For example, in the event of unexpected contingencies, a pilot may decide to spontaneously switch to an entirely new route; the new trajectory, however, remains valid within the context of the task. These versatile guidance capabilities require reasoning about the larger geographical space and task, while at the same time taking into account the maneuvering capabilities and various effects of atmospheric conditions on behavior.
Dynamical forms of spatial behavior like those found in piloting or sports are different from the navigation problems often studied in the field of spatial cognition. To set these apart, the term guidance is used in this paper. The spatial guidance problem can be defined as the problem of how to move our own bodies or steer a vehicle dynamically in a geographical environment. The general problem for self motion or vehicle steering is the same. Like navigation, guidance requires planning a future trajectory. Without planning, it is not possible to take into account the long term outcome of the present behavior and modify it to achieve the most desirable outcome. In this paper the term guidance is used to emphasize the dynamical dimensions that get added to the geometrical and topological dimensions of navigation. In guidance problems, the path, in addition to having to satisfy the constraints of the geographical environment, has to satisfy the system's dynamics (laws of motion). Dynamics impose feasibility constraints on motion that are not trivial to represent using geometry or diagrams. The equations of motion, which describe the mechanical principles governing motion involve so-called derivatives (e.g. speed is the time derivative of position). Therefore, the full set of variables needed to describe a trajectory is larger than the three dimensions of Euclidean space, which are required to visualize a trajectory. To make matters even more complex, because of the differential equations governing motion (e.g. Newton's second law), this higher dimensional space has a geometry that is not Euclidean, i.e. the shortest path is not a straight line.
Several examples can be used to illustrate activities that engage and depend on a combination of fine-tuned control and cognitive functions. Advanced spatial skills are more typically found in competitive or extreme situations that engage both our bodies and minds. They are common for athletes, acrobats, dancers, or pilots. For example, in downhill skiing it is necessary to negotiate the terrain and the gates, while anticipating the effects of an action on the future portion of the course – the skier uses her knowledge of the terrain to determine how to cross each gate in a way that maximizes the immediate performance but also in a way that will put her in a favorable state for the oncoming portion of the course. Furthermore, many applications involve problems with only partial knowledge. For example, the environment may not be fully known, and elements of the task or environment may change over time. Success under such challenging conditions requires a strategy that allows for reactive behaviors and for taking into account their consequences in the larger plan. Therefore a successful strategy must be based on an understanding of the effect of actions in the immediate environment as well as an understanding of the larger task requirements and objectives. The complexity of these decision problems and the fact that pilot or athlete must make split-second decisions, suggests that there are fundamental mechanisms in spatial cognitive functions that remain unknown.
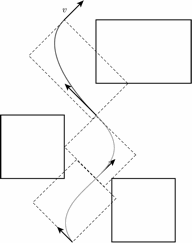
Figure 1 – Obstacle-field guidance task showing one of many possible trajectories. Also shown is an arbitrary partitioning of the space (dashed boxes) that highlights the idea that the larger, high-dimensional, continuous decision problem could be decomposed into smaller, more tractable ones. This decomposition, besides making the decision problem more tractable (from a sensory and computational standpoint), also provides a basis to represent the high-dimensional problem in a lower-dimensional form that is amenable to performing the type of spatial reasoning involved in tactical planning or adaptation.
The study of agility tends to focus on fine-tuned sensory-motor skills needed to precisely follow a desired path. These skills, however, are not sufficient for agile capabilities. Sensory-motor skills must be integrated with cognitive functions. Ultimately, agility requires both physical and mental faculties. These two aspects of behavior have often been studied separately. In engineering, the higher-level planning and decision making functions are typically based on computational theories that do not take into account the physical layer of behavior (Belta et al. 2007), and, conversely, the sensory-motor skills rarely reach out to the higher decision level (McRuer and Krendel 1974, Holding 1981, Jagacinski and Flach 2003). In cognitive science, there is a similar chasm between low and high levels. The understanding of agile spatial skills in general, and these previously unknown spatial cognitive functions in particular, requires an integrated approach based on the study of the type of structure that arises from the interrelationship among the dynamics, the environment and the task.
To better frame the following discussion, it is helpful to provide a technical description of the spatial guidance problem. For this purpose, consider a simple, planar obstacle-field like that depicted in Figure 1. The task is to travel across this field in minimum time, while avoiding the obstacles. The behavior is described by a trajectory. Even this simple problem is sufficient to describe challenges associated with guidance and is a prototype for more complex problems. Compared to a navigation task, in a dynamic guidance task, the spatial and temporal variables describing the behavior are coupled by the equations of motion. Due to these dynamical constraints, it is not possible to account for the topological layout independently from the dynamic behavior, and, vice-versa, it is impossible to drive the movement without understanding the future effects of these actions. A possible approach is to break down the problem into smaller, more tractable ones. But how can this be done in a way that, at the same time, preserves the relationships between global and local problem characteristics (consistency), and is tractable for spontaneous behavior?
This example highlights the fact that guidance behavior requires simultaneously dealing with issues associated with the physical constraints of movement and its control (which is a continuous process) and the issues related to spatial and tactical reasoning (which are best understood using finite and discrete representations). This dichotomy between the physical implementation and the conceptualization of behavior raises questions that go beyond traditional spatial cognition. The fact that humans and some animals can perform such tasks suggest that they possess a system to conceptualize spatial behavior that preserves the interrelation between movement dynamics and geometry and topology of the environment.
This gap in our understanding affects both our ability to engineer systems that show adaptive and agile behavior and our understanding of more complex human and animal behaviors. Existing guidance systems can effectively compensate for small perturbations but lack the type of knowledge-based adaptability and tactical decision making based on an understanding of space from the perspective of dynamics. Similarly, in spatial cognition, the lower-level motor theories and theories of spatial cognition are poorly integrated.
Hierarchical models based on levels of description can help relate lower-level control to higher, cognitive levels. However, without a rigorous understanding of the fundamental principles to motivate these hierarchies, such models dismiss important connections between levels (Simon 1962) and also miss the properties that may be relevant to functional aspects. The cognitive functions associated with learning, adaptation and spatial and tactical decision making must come about as properties of the system. For example, the strategies used in some forms of behaviors must exploit organizational principles that are inherent to the problem makeup, i.e. the way the system dynamics, environment and operational conditions interact. Therefore, to begin to understand the cognitive dimensions supporting agile guidance skills, requires understanding structural properties of behavior from a dynamical systems standpoint.
This paper is organized as follows. In section 2 I describe the engineering background to spatial guidance and use this perspective to describe the gap between lower and higher levels of control. Section 3 uses a linguistic analogy to provide a broader perspective on cognitive functions in spatial behavior. This makes it possible to understand spatial skills within the conventional notion of intelligence. It also allows a better appreciation for the type of cognitive functions involved in spatial behavior and their relationships to other areas of cognition. The section discusses briefly matters traditionally related to spatial behavior, starting with perceptual and sensory guidance modalities and followed by a brief reference to the concept of a cognitive map. This section concludes by discussing the diversity of forms of spatial behavior, a reality that underscores the difficulty of studying spatial cognition as a single unified phenomenon. Section 4 describes fundamental characteristics of the guidance problem. First it describes guidance as a planning problem, and then describes how dynamics affect that problem. Finally, section 5 concludes with a discussion regarding how to make the theoretical principles used in engineering application relevant to cognitive science.
Guidance and Control Engineering
An area of study where one is eventually confronted with notions surrounding human or animal spatial skills lies within engineering problems that aim at reproducing such skills, including robot control and autonomous vehicle guidance. These applications highlight the shortcomings of engineering methods in enabling human-like capabilities. However, the gaps are not clearly understood, and they are mostly noted through the limited capabilities of these systems in comparison to human pilots. A first step therefore is to be able to combine engineering methodologies and cognitive science knowledge in a multi-disciplinary field.
Engineering Background
Historically, guidance problems in engineering started in aerospace with the advent of missiles and rockets (Bryson 1996). The techniques that were developed to solve such guidance problems were mostly based on numerical optimization techniques. Limitations in these earlier applications have often been viewed in terms of computational limitations. Today's guidance problems have seen a renewed attention, in part due to the surge in robotics and autonomous vehicles. The expectations are that such systems perform closer to human pilots or operators, and can better integrate with human-operated vehicles and plants. However, computational concerns are still an issue, and it is more obvious than ever that there exists a gap in our fundamental understanding of guidance skills in particular and spatial cognition in general.
For the autonomous control of vehicles, be they robotic, automotive, or aeronautic, spatial control can be mathematically formulated using principles of optimal control. However, a trajectory optimization problem that takes into account all elements of the problem, including spatial topology, vehicle dynamics and task specifications, leads to a program that is computationally intractable for real time solution. This comes at odds with the seamlessness and flexibility seen in human or animal performance. Whereas a spatial control problem can be formulated using traditional language of mathematical optimization, its translation into a so-called mathematical program, which can be solved using a computer, is very tedious. It requires exhaustive enumeration and codification of the problem's specifications in a way that does not take advantage of the type of structure, which seems to play a fundamental role in human and animal skills and that we are beginning to describe here.
Practical solutions currently proposed in applications use approximations and heuristics to allow mathematical formulation and help alleviate computational issues. The heuristics, however, do not exploit deeper structure in the interaction between environment and dynamics. This leads to a dichotomy in dealing either with spatial complexity or dynamical complexity. Robotics have traditionally emphasized interactions with the environment (Latombe 1991), whereas in aerospace the emphasis has been more on dynamics (Bryson 1996). Applications involving robot manipulators (e.g. in manufacturing settings), or ground vehicles operating within urban environments, have a structure that can be more easily codified than those involving vehicles with broad maneuvering range, like helicopters, evolving in unstructured environments under a broader range of operational conditions. In a simply structured environment, robot behavior can be programmed using languages of motion description that are based on relatively simple logical and symbolic operations (Brocket 1993). For applications, which do not have an obvious structure, the same methods do not allow sufficiently rich language to describe the complete solution space and capture the range of phenomena that can occur. For the latter, it is currently impossible to achieve the type of response flexibility and adaptability needed for agile behavior.
Gap between Low and High-Level Spatial Skills
The gap between natural and engineered systems reflects the gap in our understanding between motor skills and higher-level cognitive functions. Studying guidance skills in all detail encompasses fine motor skills as well as strategic decision making, reasoning, and learning. This, in turn, requires an understanding of cognitive functions similar to other intelligent behaviors. For example, cognitive functions provide an understanding of the task. But what are these functions exactly? How can a task be represented in its totality to allow reasoning and tactical decisions while simultaneously encoding details related to the dynamics of the behavior? These questions are related to other areas of reasoning and planning.
Existing Relationships to Cognitive Science
This section provides a brief overview of some known relationships between spatial behavior and cognitive science. Spatial Intelligence (body kinesthetic) has been considered one of several forms of intelligence (Gardner 1983). One can come up with many ways to connect spatial behavior with language, problem solving and reasoning. These connections run deep via early cognitive and neurobiological research. Despite these indications of spatial behavior as a higher-level function, there are many ways one can trivialize or over-reduce spatial behavior. The second part of this section looks at two of these issues. First, there is the risk of an overemphasis on sensory and perceptual explanations. And second, there is a risk of misunderstanding skills due to the broad scope in manifestation of spatial skills across species.
Spatial Behavior, Language and Intelligence
The existence of a specialized form of intelligence dealing with motion implies the existence of brain capabilities far exceeding the known sensory and cognitive functions. The fact that spatial concepts are also ubiquitous within linguistic and other intellectual—even emotional—experiences further underscores the complexity and extent of spatial cognitive functions. From a mathematical perspective, the guidance problem is a form of a sequential decision problem that can be viewed as a prototype to many decision making problems. This further suggests that the apparatus that evolved in humans and animals to provide spatial navigation and guidance of movement may be related to, and participate in, a fundamental way in other cognitive functions.
Our ability to successfully plan motion, that is to take into account the future outcome of our decisions or behaviors within the larger context of a task or problem, depends on the efficiency with which the brain can codify the interrelation between space and dynamic behavior. Similarly, this also holds for adapting plans following changes in the environment or task, or even more generally due to changes in reasoning. The type of conceptualization taking place when dealing with dynamic forms of spatial behavior is largely intuitive and unconscious. It has not been associated with the traditional body of cognitive sciences and has not been studied extensively. Existing forms of codification are mainly based on computational and logical aspects. Little is known about the relationship between dynamics of movement or motion and the symbolic and semantic aspects typically associated with cognition.
Language represents a distinctive faculty of humans and has often been used as a model for higher cognitive functions (Chomsky 2002). Language may provide a framework to describe and understand the higher-level cognitive dimensions in spatial behavior. Language and spatial behavior are both serial, have to be generated in real time and have to obey certain rules. A system working based on a codification and rules is subject to practical constraints given that the type of dynamic planning problems are complex and often computationally intractable when approached as abstract mathematical programs. A spatial language, by organizing the relationships between space and motion, would help produce coherent and agile behaviors while performing in complex and uncertain environments. It would help in the understanding of the acquisition of task-critical information by providing a system for decoding environmental cues from the perspective of action and decision-making. By abstracting and distilling details out of the complexity of all the possible dynamic interaction of the system and its environment, it would also simplify the problem of movement planning. A spatio-dynamic language would clarify the mechanisms of spatial reasoning and associated adaptive functions. A system that is structured like language would also help learning, and would support adaptation to changes in environment or task conditions. It is the combination of such cognitive functions and their integration with the sensory-motor skills that would result in what we may call spatial intelligence.
Analogy between spatial behavior and language has already been made in dance performance (Hanna 2001). Dance performances manifest the type of relationship between body motion and space where this relationship has an underlying structure. Dance choreography, provides an area where a type of spatial language has been investigated. Existing choreographic languages attempt to codify the relationship between motion and space from a systematic understanding of human movement. Yet no notation system in particular has established itself. One of the better known systems is the Laban Movement Analysis (Hodgson 2001, Newlove 2004). The lack of a commonly accepted standard system has made it difficult to preserve and duplicate dance performances (Lubow 2009). These concepts, which are built on a deeper structure in behavior are also prevalent in sports. For example, in tennis, game strategies are expressed as patterns of play. The codification of these patterns makes it possible to communicate strategies and develop training routines and drills (O'Donoghue 2001). It is interesting to note that in tennis, some people talk about the players strategic abilities as a court IQ.
However, while these concepts are attractive, it is not trivial to understand what an ideal system would look like and on what principles it would be built. The main avenues that have been dominating the study of spatial skills are on the lower level, i.e. the sensory/perceptual and on the higher level, i.e. the symbolic and computational principles. Both, however, are disconnected from the fundamental characteristics of spatial behavior. A different avenue would be to find out how space is understood from the perspective of movement. A spatio-dynamic language would have to achieve a codification of both the spatial and dynamical characteristics. Therefore it requires an understanding of the effects of dynamics on spatial planning and the deeper structure of this system, including effects of uncertainties prevalent in real-world conditions and disturbances.
Sensory and Perceptual Perspectives
Dynamic forms of behavior, and the relationship between behavior and environment has been mainly studied from sensory and perceptual perspectives. Behavior, however, is not always entirely driven by sensory information. For example, consider a problem where it is necessary to traverse complex terrain to reach a goal located beyond sight. While perceptual principles have been able to predict characteristics in spatial behavior (Lee 1998), they operate within sensory range and do not provide any basis of understanding for higher-level functions necessary for planning and spatial reasoning.
Even spatial behavior involving simple dynamics and topologies combines both sensory and planning functions. In more complex forms of spatial behavior involving vehicles with complex dynamics and challenging environments, the planning problem becomes so complex of a decision problem that cognitive functions are expected to play a significant role in making the solution tractable for real time responses. Furthermore, in uncertain and disturbed conditions, cognitive functions are required to provide the type of interactive planning and information assimilation processes needed to achieve robustness. A purely perception-based approach would be too unreliable under adverse conditions.
Cognitive Maps and the Neurobiology of Spatial Cognition
Studying spatial behavior has been an important approach to understanding the brain starting with the work of Tolman and his cognitive map (Tolman 1948) and continuing with the extensive work of O'Keefe (O'Keefe and Dostrovsky 1971) on the hippocampus and its possible role as the neuronal substrate for a cognitive map. Neurobiology of spatial cognition has so far not helped elucidate the harder questions discussed here. The classic study of spatial cognition typically focuses on how spatial information is acquired, represented, and used to guide behavior (Kitchin and Blades 2002). Simple forms of navigation, or way finding, have been the main focus of spatial cognition but without accounting for the effects of dynamics.
Tolman's concept of a cognitive map has been introduced as part of the theory of route learning (Tolman 1948) and was later extended to include other aspects of cognition (see (Johnson and Crowe 2009) for a recent reevaluation of Tolman's ideas). It has played a fundamental role in overturning the stimulus-response concepts that were dominant at the time. The cognitive map enables far more general forms of adaptation and learning mechanisms. In more recent research on the neuro-biology of spatial behavior, evidence has been reported for representations that combine velocity with place information (Sargolini et al. 2006). These higher-dimensional representations are significant here since they point to the coding of information related to the dynamics.
The Issue of Scope in Spatial Cognition
Something that often blurs the study of spatial cognition has to do with the ubiquity of spatial behavior. It presents itself in a range of different manifestations within human behavior and across species. It is often believed that many animals and even insects exhibit sophisticated spatial skills. Animals, with much smaller nervous systems than humans, for example birds or rats, are capable of what appears like sophisticated forms of spatial behaviors. Even insects have well defined spatial skills. Researchers have argued the possibility for cognition in bees (Srinivasan et al. 2006). Humans certainly stand out with their versatility. They can apply spatial skills to a broad range of tasks including competing in sports as well as piloting vehicles. When is it appropriate to speak of spatial cognition? To answer this question, we need to understand what aspects of spatial behavior rely on what type of cognitive functions. For example, the type of spatial cognition necessary for bees foraging is less sophisticated than the cognitive functions needed for bird flight.
The scope of spatial behavior and type of interactions with the environment is specific to each species' particular ecological niche and the problems they need to solve to survive. Bees can successfully navigate fields to support their pollination activity; different birds have specific foraging and migratory skills; elephants can cover distances of up to 100 miles in one day, and are known for their extensive spatial memory needed to survive long periods of drought. Similar skills have been studied in human tribes.
The study of spatial behavior, and the type of cognitive functions involved should account for the specific characteristics of a species' ecological niche. For highly structured niches, simple sensory (or perceptually) driven rules are sufficient to survive. There are many examples where spatial behavior is driven by sensory and perceptual processes rather than cognitive processes (cf. Gibson's theory of affordance (Gibson 1979) or Lee's General Tau theory (Lee 1998)). In fact, sensory-based, behavioral approaches have inspired successful techniques for controlling robots (cf. Intelligence Without Representation (Brooks 1991)). These techniques also highlight the limitations of sensory-based systems. A telling point is that the fundamental problem that needs to be solved by each species is different. Human skills are vastly different from the navigation skills of bees. In fact it is possible to regard an 'order of complexity' where a particular skill can be described as a special case of some higher skill level. There are capabilities in higher skill levels that cannot be extrapolated from capabilities found at lower skill levels. For example, navigation problems solved by bees are fundamentally different from the guidance problems solved by expert pilots or athletes.
Significance of Dynamics in Spatial Guidance
It is difficult to determine the cognitive processes—as well as other control and perceptual processes involved in spatial behavior—without understanding the fundamental problem the brain must solve when performing complex spatial guidance tasks. David Marr in his study of human vision advocated a research framework based on three levels of understanding: the abstract, computational theory; the representation or algorithm; and the hardware (i.e. biological) implementation (Marr 1982). The study at the abstract, computational level is meant to provide fundamental insights into the problem that is being solved by the brain. The study at this level is generally based on some fundamental theory. In vision, Marr uses principles of information theory (Marr and Poggio 1979). Spatial behavior, being multifaceted, makes it more difficult to reduce the problem to a single principle. However, one approach that is both fundamental and mathematically rigorous is to study behavior as a trajectory planning problem. Furthermore, since movement, or motion, has to obey dynamical principles, the trajectory planning problem is often cast within the more general framework of dynamical and control theory. The following section describes how this framework can be made relevant to spatial cognition.
Spatial Behavior as a Planning Problem
Deliberate spatial behaviors unfold sequentially and, for most guidance problems of practical relevance, actions cannot be determined in a reactive process (i.e. stimulus-response). Actions must be taken based on some form of understanding of the consequences of the action on future behavior. This is due to the fact that a given action will have a specific impact in the state and context within which future decisions will be taken and, hence, will affect the overall performance. Ideally, decisions would have to be based on their effects on a full trajectory history leading all the way to the goal. Such a process is unrealistic, given the limited decision time and the often incomplete knowledge. Decision processes that are based on prediction of future behavior are usually called planning. Navigation is often used as a metaphor for planning.
The concept of a cognitive map has served as a platform for studying navigation as a planning process. In Plans and the Structure of Behavior (Miller et al. 1960), the authors propose that planning is what distinguishes a cognitive study of behavior from a behavioral study of behavior. Planning concepts have been applied to a range of areas of human behavior from motor skills to speech and language. Guidance is important as a problem in its own right as well as in its broader ramification to other cognitive dimensions. In cognitive science, the planning problem specific to spatial behavior is often treated in an abstract way (Dorner and Schaub 1994). Similarly, the analogy among cognitive functions through planning is often very general. Going beyond this abstract, conceptual level requires understanding of the deeper structure in spatial behavior and the role this structure plays in the planning process and the general principles that organize spatial behavior. In particular, one aspect that has been overlooked is the effects of dynamics.
Dynamics make the basic planning problem much harder to study without advanced mathematical knowledge. Dynamics changes the planning problem in at least three ways: it increases the dimensions of the problem space, taking it beyond the two or three dimensions of geographical space; it imposes feasibility constraints that an admissible trajectory must satisfy (differential constraints that arise from the differential equations relating spatial and temporal) and it furthermore changes the notion of distance (which is no longer Euclidean). It is important to stress that these effects are inherent to the nature of the planning problem (not an artifact that comes from the solution method) and, therefore, are fundamental characteristics that have to be dealt with.
Types of Planning Problems
Navigation or guidance problems can take a variety of forms depending on the type of environment, the available knowledge, and the dynamics underlying the behavior. Planning routes in mazes or obstacle fields—like those Tolman's rats had to negotiate—represents the most basic prototype for a planning problem. In cognitive science this type of navigation is typically called way finding. In robotics literature, it is called path planning. It is typically presented as the problem of determining a collision-free path between two points in a planar or three-dimensional environment (Latombe 1991). These basic forms of planning problems can be easily discretized based on geometry (cf. visibility graph (de Berg et al. 2008)) and can be solved using a shortest-path algorithm for which there exist many heuristic techniques.
Dynamical forms of spatial behavior take place in a continuous space-time. Neither the temporal nor spatial dimensions are discretized in an obvious manner. Furthermore, as mentioned previously, the solution space needed to represent such a trajectory must have more than the three dimensions. This space is generally not Euclidean, therefore notions of distance do not have simple geometries (e.g. the shortest distance path between two points is the straight line in Euclidean space). These dynamical planning problems do not have an obvious structure that can be exploited in their representation. Therefore, to understand how a dynamical planning problem can be abstracted into a problem with a useful structure, requires an understanding of the intricate mathematics of high-dimensional nonlinear systems. There are certainly degrees to which dynamics matter in behavior. For example, it is possible to conceive of systems that are weakly dynamic, which can be successfully approximated using a basic topological planning problem. This may help explain why not all forms of spatial behavior involving dynamics require the same cognitive capabilities and why the bee's guidance problem can be wrongly brought in analogy to the guidance problem a pilot faces—even though both involve flight dynamics—the type of guidance problems are dramatically different due to the maneuvering range and the type of environment in which these capabilities are deployed.
Perspectives on Dynamics in the Planning Problem
Nature provides an infinite array of dynamical systems illustrating the type of behaviors and effects that are associated with these systems. For example, patterns in fluid flow provide a visual insight of some of the effects that are inherent to a dynamical system. But it is important to realize that similar effects, most often invisible to our senses, take place all around us. In the context of spatial behavior the dynamical principles that govern the system's behavior, e.g. the vehicle or body motion, play a fundamental role in determining the decision making process. Compared to other decision making problems, in guidance behavior one is forced to collaborate with the dynamical effects. Therefore understanding the type of structure associated with the movement mechanics and dynamics is fundamental to understanding the human control and cognitive processes.
Conclusions
Planning is central to decision making, and guidance is a form of decision making. However, it is important to realize that when it comes to dynamical forms of spatial behavior, a human or an animal is less a decision making agent in the traditional sense. Rather, achieving agile spatial skills requires understanding what can be naively described as the flow properties of behavior. These properties arise from the interaction between the dynamics and the environment. Therefore guidance decisions involve interacting with the system within these behavioral structures. Sports provide a good example for this perspective since the body is driven to the physical limits and hence dynamics heavily constrain the behavior. One of the brain's key roles in these tasks is to understand this system and interact with it based on the choices that present themselves within the particular characteristics of that dynamic system. Furthermore, beyond just constraining behavior and establishing structure, these characteristics also provide a system to organize behavior from a higher level, i.e. they provide a basis to build a decision hierarchy which ultimately defines the higher level cognitive functions. This perspective is different from the traditional planning paradigm, which, often due to its simple structure, has hierarchies that are not necessarily related to deeper structural characteristics and functional properties and therefore does not provide much information about the functional characteristics of cognitive processes.
The fundamental challenge in better understanding spatial cognition and enabling engineering methodologies depends on our understanding of the structure of behavior and more specifically the effect of dynamics in this structure. Dynamical systems theory, which was developed from classical mechanics, has in the last century found increasing applications to non-mechanical systems. Such systems include, social, economical, and biological study. This broadening of the domain of dynamical systems has led to problems of greater mathematical complexity that are far less trivial to model and study analytically. Nevertheless, the increase in complexity and broadening of scope led to a change in perspective from a quantitative to a qualitative study (Hirsch 1984). Mathematicians, starting with Poincaré, developed methods to analyze and describe the patterns and structure of behavior of complex systems. These methodologies gave a new paradigm to studying high-dimensional, nonlinear dynamical systems providing important insights into behavior.
Revisiting Optimal Control and Dynamical Systems Theory
Optimal control, or more generally the principles of optimality, developed in part to support the design of guidance laws for aircraft and missiles (Bryson 1996). In these engineering applications, optimality principles have a practical purpose; they provide tools to determine trajectories between initial and terminal conditions with properties that are desirable from an operational standpoint, like minimizing time or energy. The application of optimality principles to studying human behavior often faces the debate of optimization: a result or a mechanism? (Staddon and Hinson 1983). As pointed out by Staddon,
"Optimality models provide a tolerably good picture of what animals manage to achieve; but a poor picture of how they actually do it." (p. 976) Furthermore, "Optimality theory in general is not testable, since any experimental result can be expressed as the optimal solution to some problem; what is testable is constrained optimization, the idea that animals behave optimally subject to specified constraints." (p. 976)
Optimal control, however, is not restricted to its role as a computational or decision making principle. The theory of optimal control is best applied in combination with dynamical systems theory. Applied as a single mathematical framework, optimal control provides a way to understand behavior when decisions are made in a way that exploits the dynamical capabilities and characteristics of the system. It is in this sense that optimal control is most useful as a framework to study human or animal behavior. High-performance athletes are able to operate close to the limits of their physical performance. Similarly, pilots can drive their vehicles to their mechanical limits. If a human pilot or athlete is capable of optimal behavior, the processes involved in guidance behavior have to deal with these dynamical dimensions. Given a particular form of spatial behavior taking place at a particular level of performance, optimal control and dynamical principles provide a mathematical framework to explicitly study the properties that are inherent to dynamical systems. In particular, optimal control provides a way to use a single framework to study behavior at the motor-control level. More specifically, studying the structures that arises from the interplay of dynamics and environment provides relevant information for the sensory and perceptual functions. In turn, these structures are relevant to the organization of behavior, all the way to the tactical planning and spatial reasoning. All these questions can be studied under a unified framework.
Dynamical Systems and Cognition
An example where concepts form dynamical systems have been used in cognition is in Thelen's work on the development of motor skills in infants (Thelen et al. 1994). The infant's behavior during early development is studied by examining the dynamical pattern of the infant's body. The development of motor skills is described as changes in these patterns. Thelen proposed that the infant's cognitive functions develop through a process of learning categories combining perceptual and action patterns. Moreover, she suggested that the principles of a dynamical system provide a theoretical framework to explain embodied cognition, first by providing the modeling and analysis tools necessary to describe the development of motor skills and perception, and second by providing a principle explaining the development of categories. She proposed that the categories, which are described using the language of dynamical systems, represent building blocks in the development of abstraction and eventually language.
For dynamical systems, in particular spatial and operational environments, the types of patterns in behavior are relevant in the sense that they convey information about the interactions between the dynamics and the environment. Even though the system could in theory exhibit a broad variety of behaviors, when operating in particular spatial environments, the behavior will tend to cluster in specific ways. These qualitative features are the manifestations of the interaction effects between the dynamics and the environment. From a mathematical standpoint, these features describe a lower-dimensional representation of the problem. Therefore they can help in understanding the type of abstraction that can be used when dealing with these high-dimensional planning problems. For example, it is foreseeable that features can be used to develop a language for spatial behavior. Finally, these features can also help to identify and make understandable functional aspects of behavior, such as mechanisms that are used in adaptation and learning.
References
Belta C, Bicchi A, Egerstedt M, Frazzoli E, Klavins E, Pappas G (2007) Symbolic planning and control of robot motion. IEEE Robot Autom Mag 14:61–70
Brockett RW (1993) Hybrid models for motion control systems, in Trentelman HL, Willems JC (1993) Essays on control: perspectives in the theory and its applications. Birkhauser, Boston, MA
Brooks RA (1991) Intelligence without representation. Artif Intell 47:139–159
Bryson AE (1996) History of optimal control. IEEE Contr Syst Mag pp 26–33
Chomsky N (2002) Syntactic structures. Walter de Gruyter
de Berg M, van Krefeld M, Overmars M, Schwarzkopf O (2008) Computational geometry: algorithms and applications. Springer, New York, NY
Dörner D, Schaub H (1994) Errors in planning and decision-making and the nature of human information processing. Appl Psychol 43:433– 453
Gardner H (1983) Frames of mind: the theory of multiple intelligences. Basic Books, New York, NY
Gibson JJ (1979) The ecological approach to visual perception. Houghton Mifflin, Boston, MA
Hanna J (2001) The language of dance. JOPERD–The Journal of Physical Education, Recreation & Dance, 72:40-45
Hirsch M (1984) The dynamical systems approach to differential equations. Bull Amer Math Soc 11:1-64
Hodgson J (2001) Mastering movement: the life and work of Rudolf Laban. Routledge, New York, NY
Holding DH (1981) Human skills. Wiley series on studies in human performance. John Wiley & Sons
Jagacinski R, Flach J (2003) Control theory for humans: quantitative approaches to modeling performance. CRC Press
Johnson A, Crowe D (2009) Revisiting Tolman, his theories and cognitive maps. Cog Crit 1:43-72
Kitchin R, Blades M (2002) The cognition of geographical space. IB Tauris Co Ltd, New York, NY
Latombe J (1991) Robot motion planning. Kluwer Academic Publishers, Boston, MA
Lee DN (1998) Guiding movement by coupling of taus. Ecol Psychol 10:221–250
Lubow A (2009) Can modern dance be preserved? The New York Times Magazine, pp 38–43
Marr D (1982) Vision: a computational investigation into the human representation and processing of visual information. W. H. Freeman and Company, San Francisco, CA.
Marr D, Poggio T (1979) A computational theory of human stereo vision. P Roy Soc Lond B Bio 204:301–328
McRuer D, Krendel E (1974) Mathematical models of human pilot behavior. Technical Report AGARD-AG-188, AGARD
Miller GA, Pribram KH, Galanter E (1960) Plans and the structure of behavior. Holt, New York, NY
Newlove J (2004) Laban for all. Routledge, New York, NY
O'Donoghue P, Ingram B (2001) A notational analysis of elite tennis strategy. J Sport Sci 19:107-115
O'Keefe J, Dostrovsky J (1971) The hippocampus as a spatial map. preliminary evidence from unit activity in the freely-moving rat. Brain Res 34:171–175
Sargolini F, Fyhn M, Hafting T, McNaughton B, Witter M, Moser M-B, Moser E (2006) Conjunctive representation of position, direction, and velocity in entorhinal cortex. Science 312:758–762
Simon HA (1962) The architecture of complexity. P Am Philos Soc 106: 467–482
Srinivasan M, Zhang S, Reinhard J (2006) Small brains, smart minds: vision, perception, navigation and 'cognition' in insects. International Conference on Invertebrate Vision. Cambridge University Press, Cambridge, pp 462–493
Staddon J, Hinson JM (1983) Optimization: a result or a mechanism? Science 221:976-977
Thelen E, Smith L, Lewkowicz D, Lickliter R (1994) A dynamic systems approach to the development of cognition and action. MIT Press, Cambridge, MA
Tolman TE (1948) Cognitive maps in rats and men. Psychol Rev 55:189–208

